Circular Queue Datastructure
In a normal Queue Data Structure, we can insert elements until queue becomes full. But once the queue becomes full, we can not insert the next element until all the elements are deleted from the queue. For example, consider the queue below...
The queue after inserting all the elements into it is as follows...
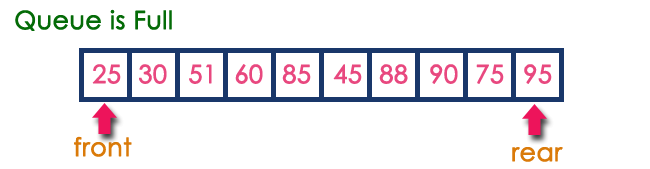
Now consider the following situation after deleting three elements from the queue...

This situation also says that Queue is Full and we cannot insert the new element because 'rear' is still at last position. In the above situation, even though we have empty positions in the queue we can not make use of them to insert the new element. This is the major problem in a normal queue data structure. To overcome this problem we use a circular queue data structure.
What is Circular Queue?
A Circular Queue can be defined as follows...
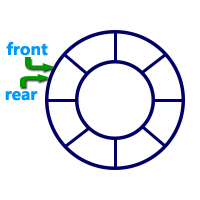
A circular queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle and the last position is connected back to the first position to make a circle.
Graphical representation of a circular queue is as follows...
Implementation of Circular Queue
To implement a circular queue data structure using an array, we first perform the following steps before we implement actual operations.
- Step 1 - Include all the header files which are used in the program and define a constant 'SIZE' with specific value.
- Step 2 - Declare all user defined functions used in circular queue implementation.
- Step 3 - Create a one dimensional array with above defined SIZE (int cQueue[SIZE])
- Step 4 - Define two integer variables 'front' and 'rear' and initialize both with '-1'. (int front = -1, rear = -1)
- Step 5 - Implement main method by displaying menu of operations list and make suitable function calls to perform operation selected by the user on circular queue.
enQueue(value) - Inserting value into the Circular Queue
In a circular queue, enQueue() is a function which is used to insert an element into the circular queue. In a circular queue, the new element is always inserted at rear position. The enQueue() function takes one integer value as parameter and inserts that value into the circular queue. We can use the following steps to insert an element into the circular queue...
- Step 1 - Check whether queue is FULL. ((rear == SIZE-1 && front == 0) || (front == rear+1))
- Step 2 - If it is FULL, then display "Queue is FULL!!! Insertion is not possible!!!" and terminate the function.
- Step 3 - If it is NOT FULL, then check rear == SIZE - 1 && front != 0 if it is TRUE, then set rear = -1.
- Step 4 - Increment rear value by one (rear++), set queue[rear] = value and check 'front == -1' if it is TRUE, then set front = 0.
deQueue() - Deleting a value from the Circular Queue
In a circular queue, deQueue() is a function used to delete an element from the circular queue. In a circular queue, the element is always deleted from front position. The deQueue() function doesn't take any value as a parameter. We can use the following steps to delete an element from the circular queue...
- Step 1 - Check whether queue is EMPTY. (front == -1 && rear == -1)
- Step 2 - If it is EMPTY, then display "Queue is EMPTY!!! Deletion is not possible!!!" and terminate the function.
- Step 3 - If it is NOT EMPTY, then display queue[front] as deleted element and increment the front value by one (front ++). Then check whether front == SIZE, if it is TRUE, then set front = 0. Then check whether both front - 1 and rear are equal (front -1 == rear), if it TRUE, then set both front and rear to '-1' (front = rear = -1).
display() - Displays the elements of a Circular Queue
We can use the following steps to display the elements of a circular queue...
- Step 1 - Check whether queue is EMPTY. (front == -1)
- Step 2 - If it is EMPTY, then display "Queue is EMPTY!!!" and terminate the function.
- Step 3 - If it is NOT EMPTY, then define an integer variable 'i' and set 'i = front'.
- Step 4 - Check whether 'front <= rear', if it is TRUE, then display 'queue[i]' value and increment 'i' value by one (i++). Repeat the same until 'i <= rear' becomes FALSE.
- Step 5 - If 'front <= rear' is FALSE, then display 'queue[i]' value and increment 'i' value by one (i++). Repeat the same until'i <= SIZE - 1' becomes FALSE.
- Step 6 - Set i to 0.
- Step 7 - Again display 'cQueue[i]' value and increment i value by one (i++). Repeat the same until 'i <= rear' becomes FALSE.
Implementation of Circular Queue Datastructure using array - C Programming
#include<stdio.h>
#include<conio.h>
#define SIZE 5
void enQueue(int);
void deQueue();
void display();
int cQueue[SIZE], front = -1, rear = -1;
void main()
{
int choice, value;
clrscr();
while(1){
printf("\n****** MENU ******\n");
printf("1. Insert\n2. Delete\n3. Display\n4. Exit\n");
printf("Enter your choice: ");
scanf("%d",&choice);
switch(choice){
case 1: printf("\nEnter the value to be insert: ");
scanf("%d",&value);
enQueue(value);
break;
case 2: deQueue();
break;
case 3: display();
break;
case 4: exit(0);
default: printf("\nPlease select the correct choice!!!\n");
}
}
}
void enQueue(int value)
{
if((front == 0 && rear == SIZE - 1) || (front == rear+1))
printf("\nCircular Queue is Full! Insertion not possible!!!\n");
else{
if(rear == SIZE-1 && front != 0)
rear = -1;
cQueue[++rear] = value;
printf("\nInsertion Success!!!\n");
if(front == -1)
front = 0;
}
}
void deQueue()
{
if(front == -1 && rear == -1)
printf("\nCircular Queue is Empty! Deletion is not possible!!!\n");
else{
printf("\nDeleted element : %d\n",cQueue[front++]);
if(front == SIZE)
front = 0;
if(front-1 == rear)
front = rear = -1;
}
}
void display()
{
if(front == -1)
printf("\nCircular Queue is Empty!!!\n");
else{
int i = front;
printf("\nCircular Queue Elements are : \n");
if(front <= rear){
while(i <= rear)
printf("%d\t",cQueue[i++]);
}
else{
while(i <= SIZE - 1)
printf("%d\t", cQueue[i++]);
i = 0;
while(i <= rear)
printf("%d\t",cQueue[i++]);
}
}
}
Output
