Max Heap Datastructure
Heap data structure is a specialized binary tree-based data structure. Heap is a binary tree with special characteristics. In a heap data structure, nodes are arranged based on their values. A heap data structure some times also called as Binary Heap.
There are two types of heap data structures and they are as follows...
- Max Heap
- Min Heap
Every heap data structure has the following properties...
Property #1 (Ordering): Nodes must be arranged in an order according to their values based on Max heap or Min heap.
Property #2 (Structural): All levels in a heap must be full except the last level and all nodes must be filled from left to right strictly.
Max Heap
Max heap data structure is a specialized full binary tree data structure. In a max heap nodes are arranged based on node value.
Max heap is defined as follows...
Max heap is a specialized full binary tree in which every parent node contains greater or equal value than its child nodes.
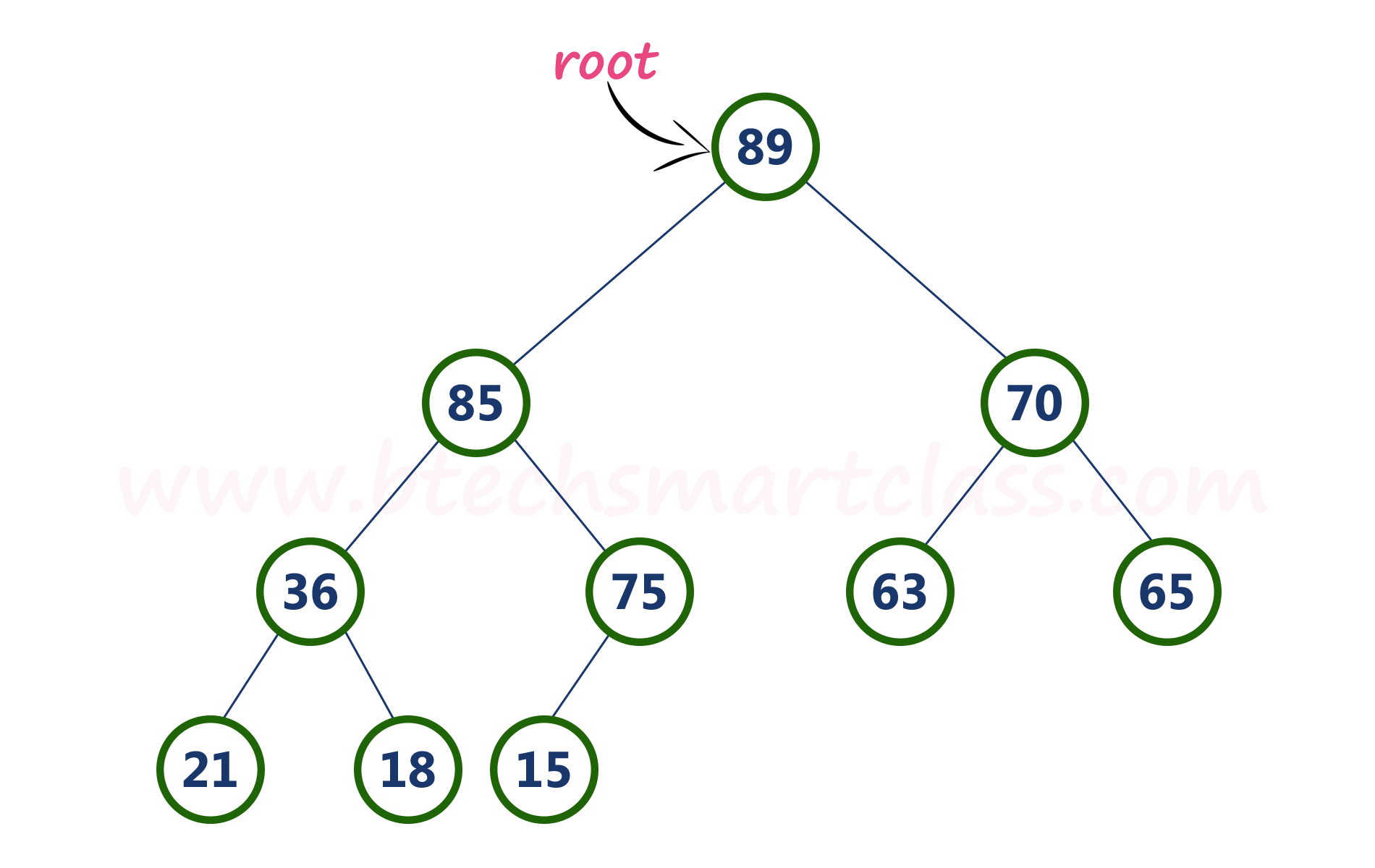
Example
Above tree is satisfying both Ordering property and Structural property according to the Max Heap data structure.
Operations on Max Heap
The following operations are performed on a Max heap data structure...
- Finding Maximum
- Insertion
- Deletion
Finding Maximum Value Operation in Max Heap
Finding the node which has maximum value in a max heap is very simple. In a max heap, the root node has the maximum value than all other nodes. So, directly we can display root node value as the maximum value in max heap.
Insertion Operation in Max Heap
Insertion Operation in max heap is performed as follows...
- Step 1 - Insert the newNode as last leaf from left to right.
- Step 2 - Compare newNode value with its Parent node.
- Step 3 - If newNode value is greater than its parent, then swap both of them.
- Step 4 - Repeat step 2 and step 3 until newNode value is less than its parent node (or) newNode reaches to root.
Example
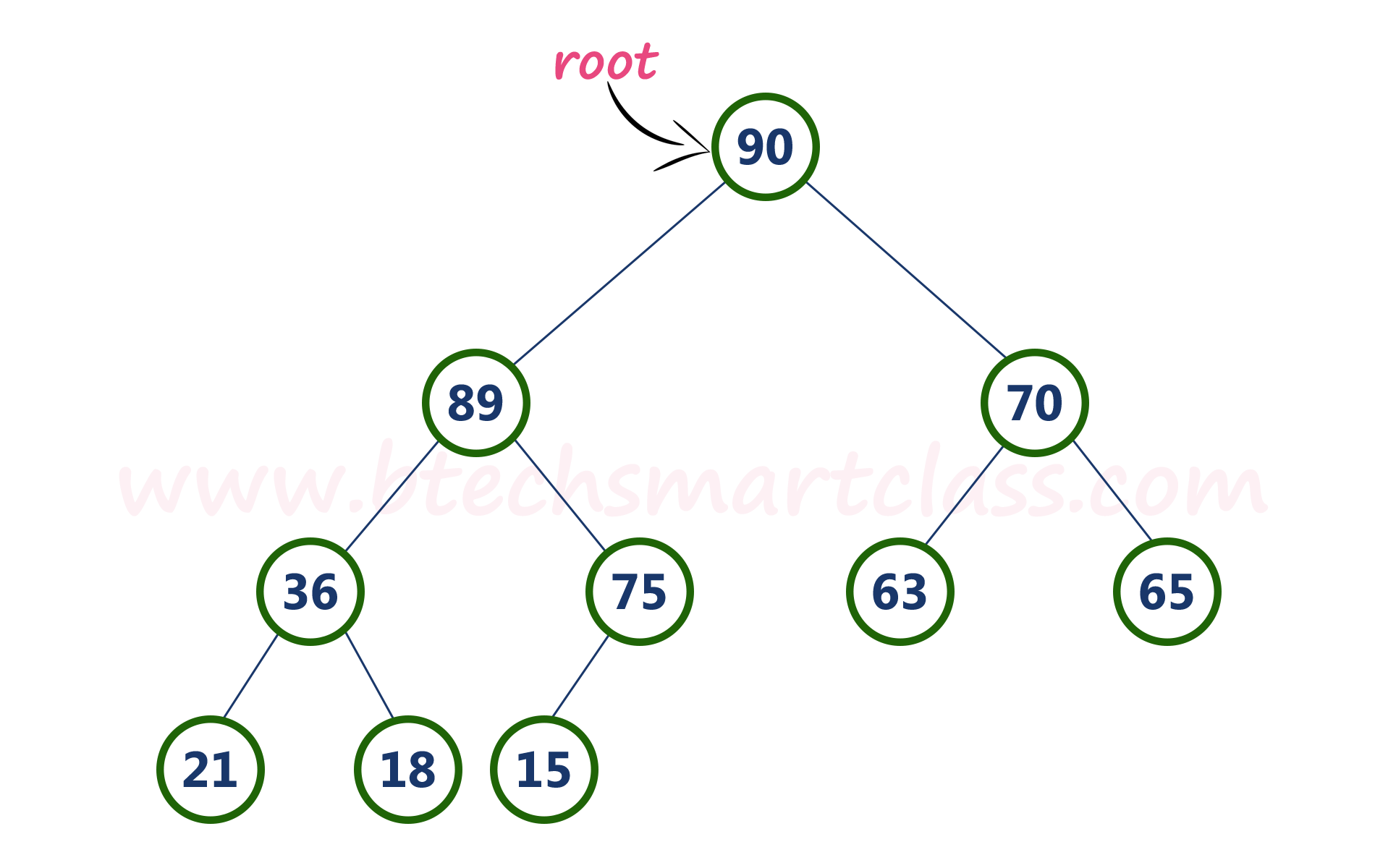
Consider the above max heap. Insert a new node with value 85.
- Step 1 - Insert the newNode with value 85 as last leaf from left to right. That means newNode is added as a right child of node with value 75. After adding max heap is as follows...
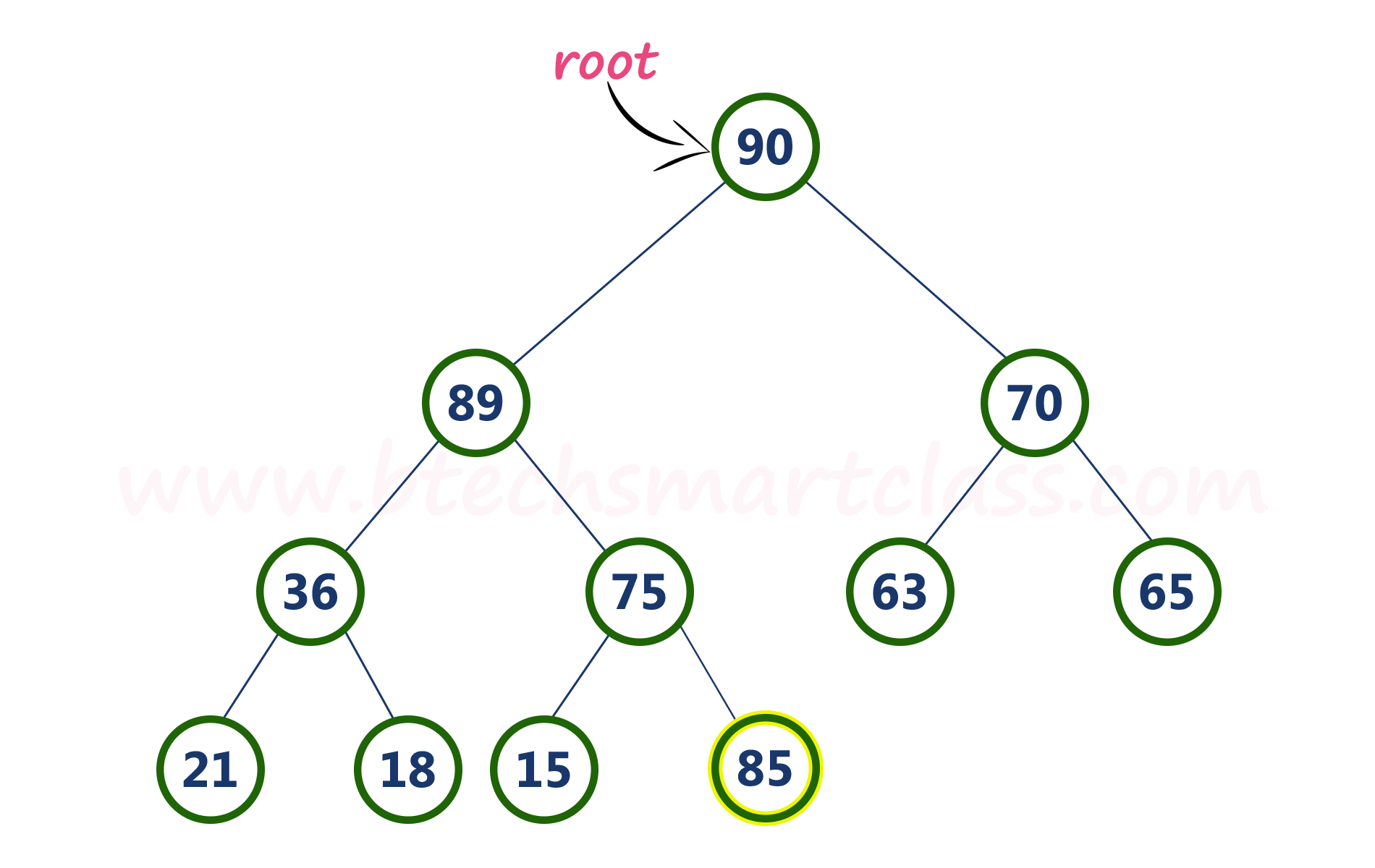
- Step 2 - Compare newNode value (85) with its Parent node value (75). That means 85 > 75
- Step 3 - Here newNode value (85) is greater than its parent value (75), then swap both of them. After swapping, max heap is as follows...
- Step 4 - Now, again compare newNode value (85) with its parent node value (89).
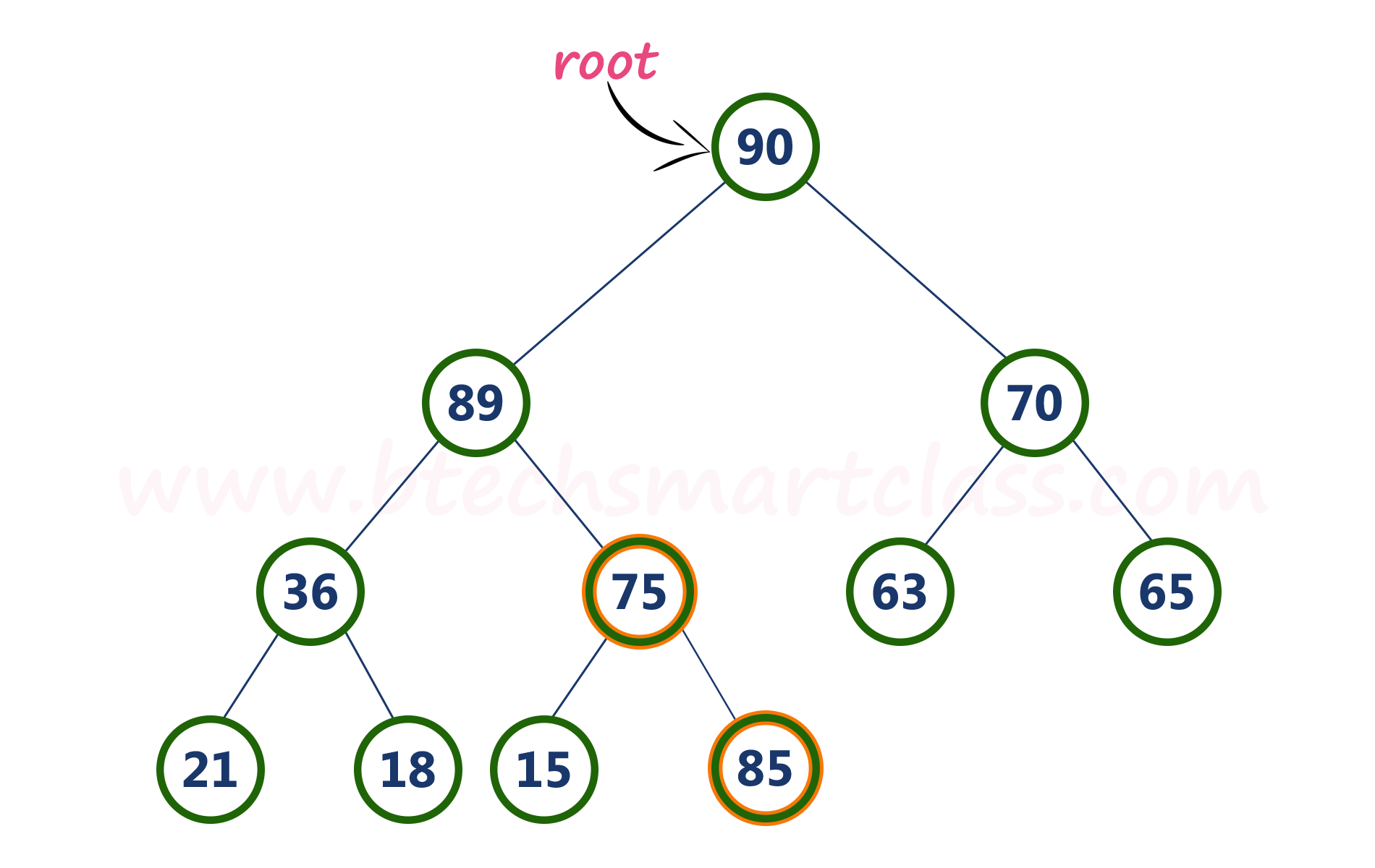
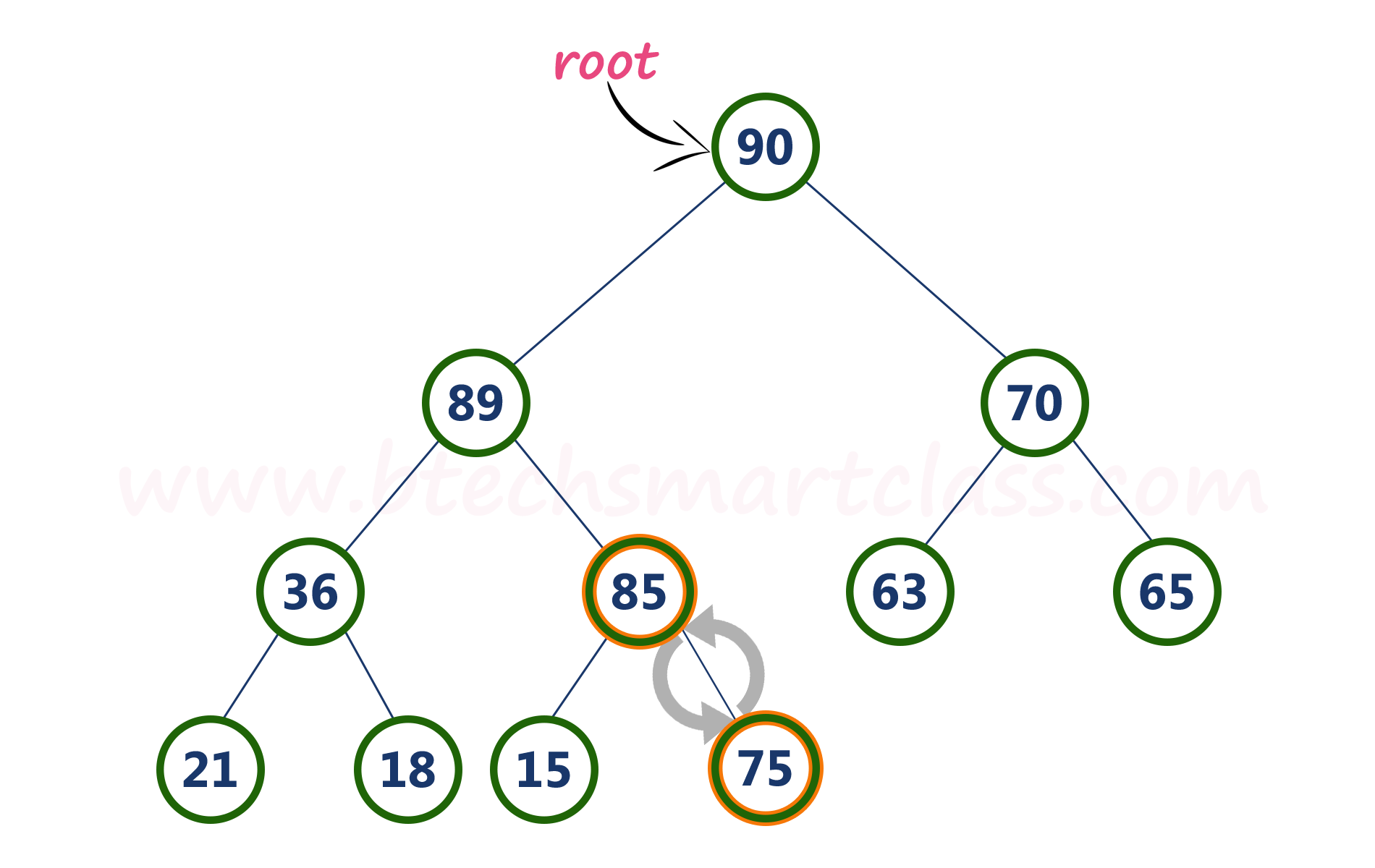
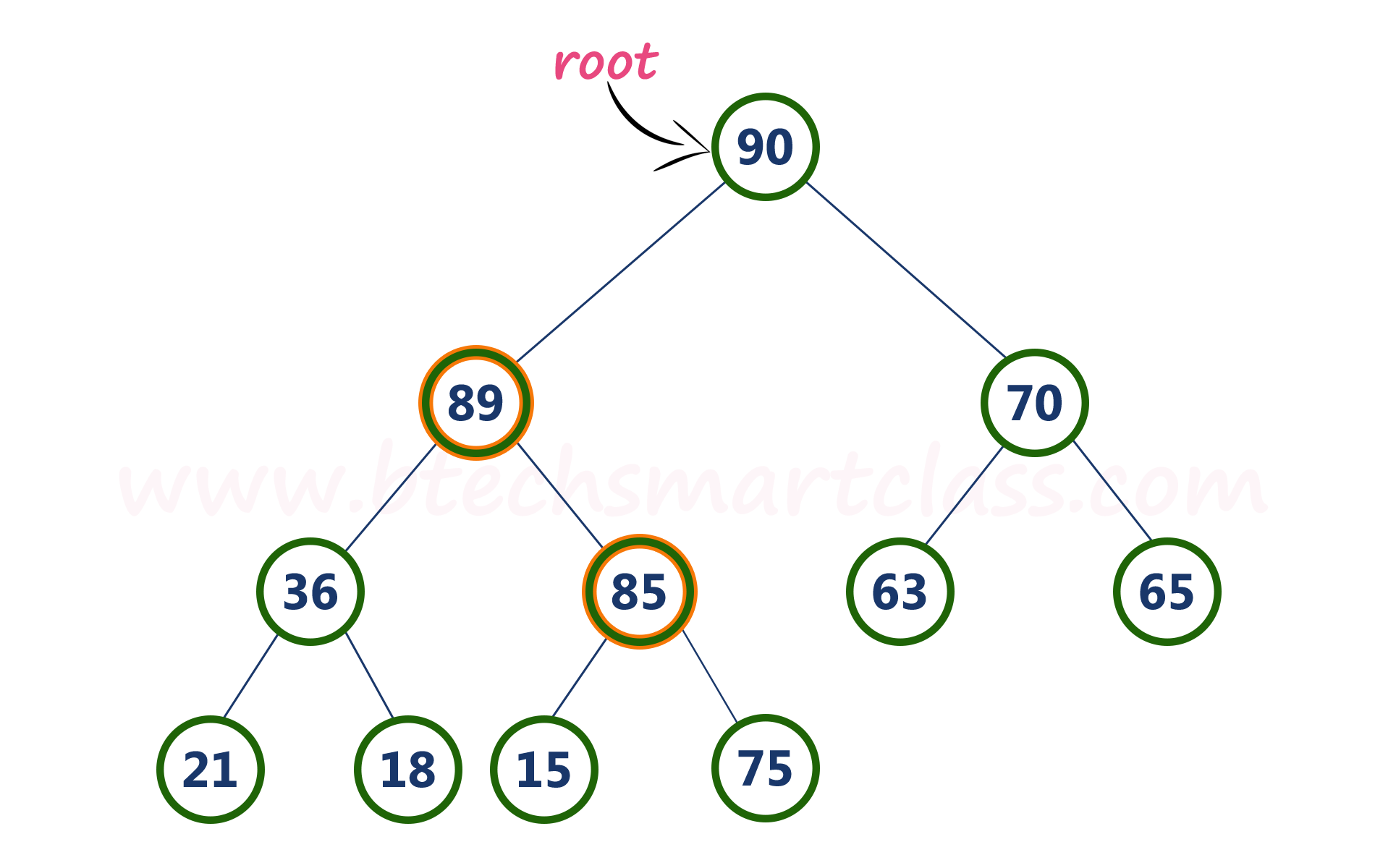
Here, newNode value (85) is smaller than its parent node value (89). So, we stop insertion process. Finally, max heap after insertion of a new node with value 85 is as follows...
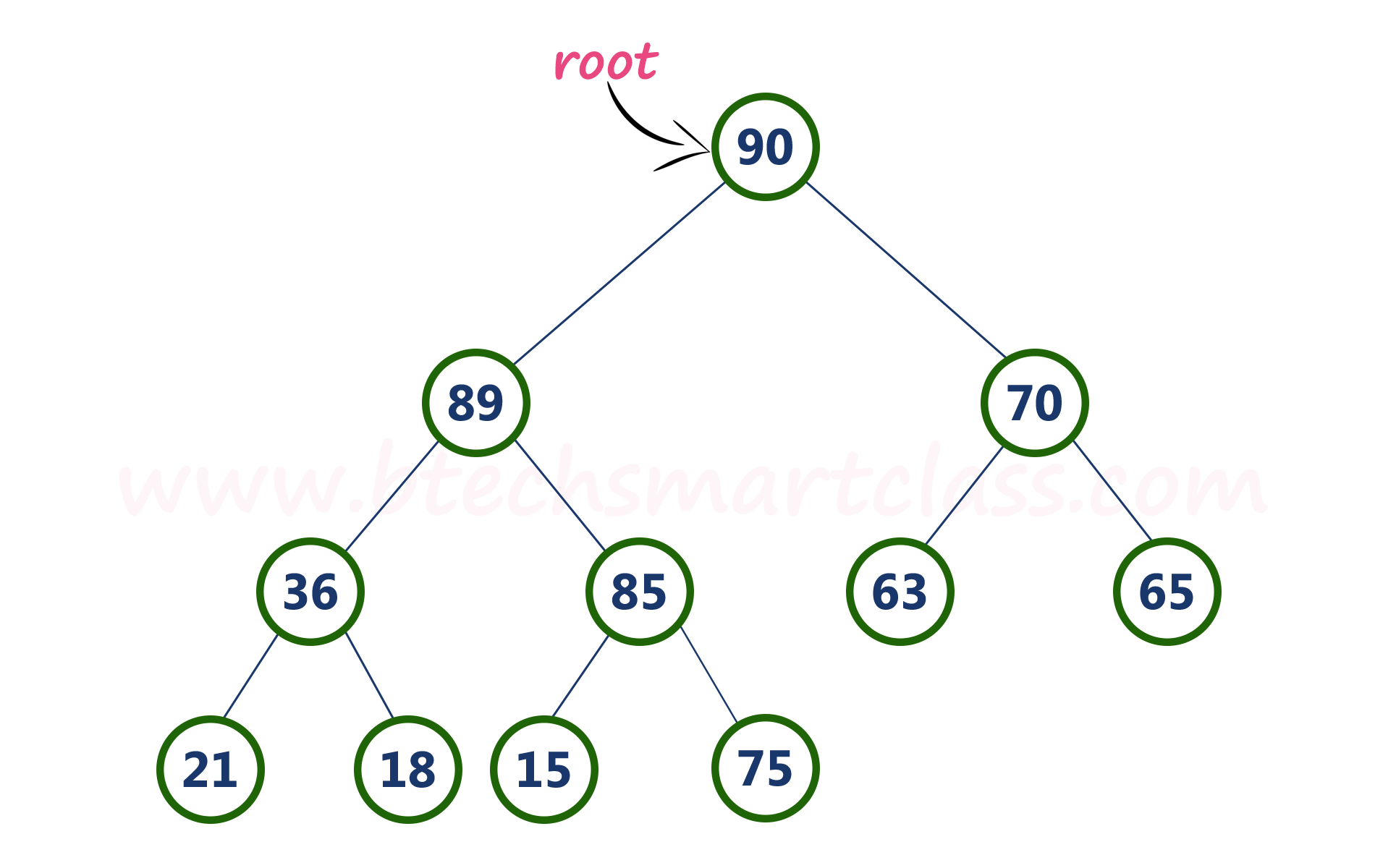
Deletion Operation in Max Heap
In a max heap, deleting the last node is very simple as it does not disturb max heap properties.
Deleting root node from a max heap is little difficult as it disturbs the max heap properties. We use the following steps to delete the root node from a max heap...
- Step 1 - Swap the root node with last node in max heap
- Step 2 - Delete last node.
- Step 3 - Now, compare root value with its left child value.
- Step 4 - If root value is smaller than its left child, then compare left child with its right sibling. Else goto Step 6
- Step 5 - If left child value is larger than its right sibling, then swap root with left child otherwise swap root with its right child.
- Step 6 - If root value is larger than its left child, then compare root value with its right child value.
- Step 7 - If root value is smaller than its right child, then swap root with right child otherwise stop the process.
- Step 8 - Repeat the same until root node fixes at its exact position.
Example
Consider the above max heap. Delete root node (90) from the max heap.
- Step 1 - Swap the root node (90) with last node 75 in max heap. After swapping max heap is as follows...
- Step 2 - Delete last node. Here the last node is 90. After deleting node with value 90 from heap, max heap is as follows...
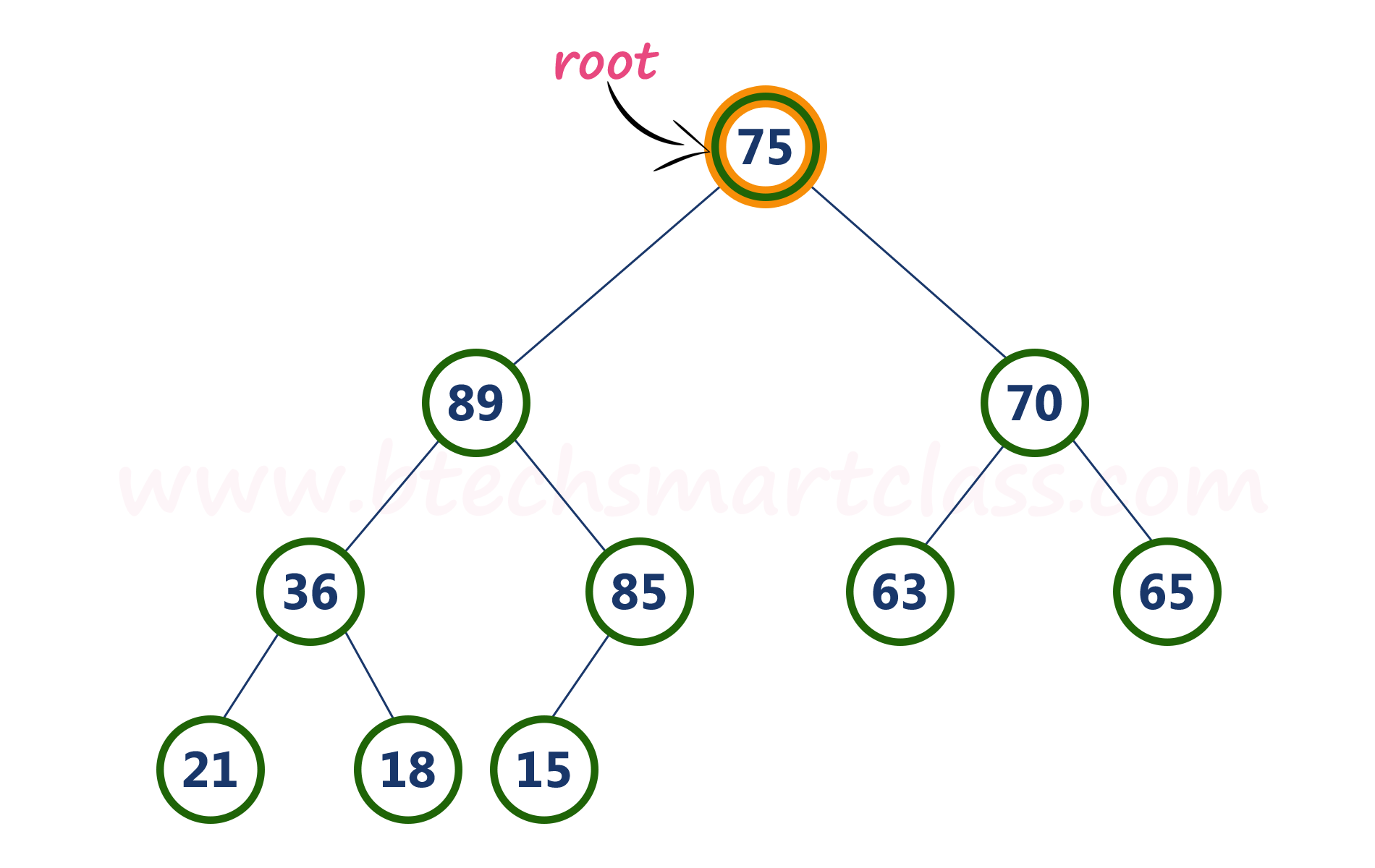
- Step 3 - Compare root node (75) with its left child (89).
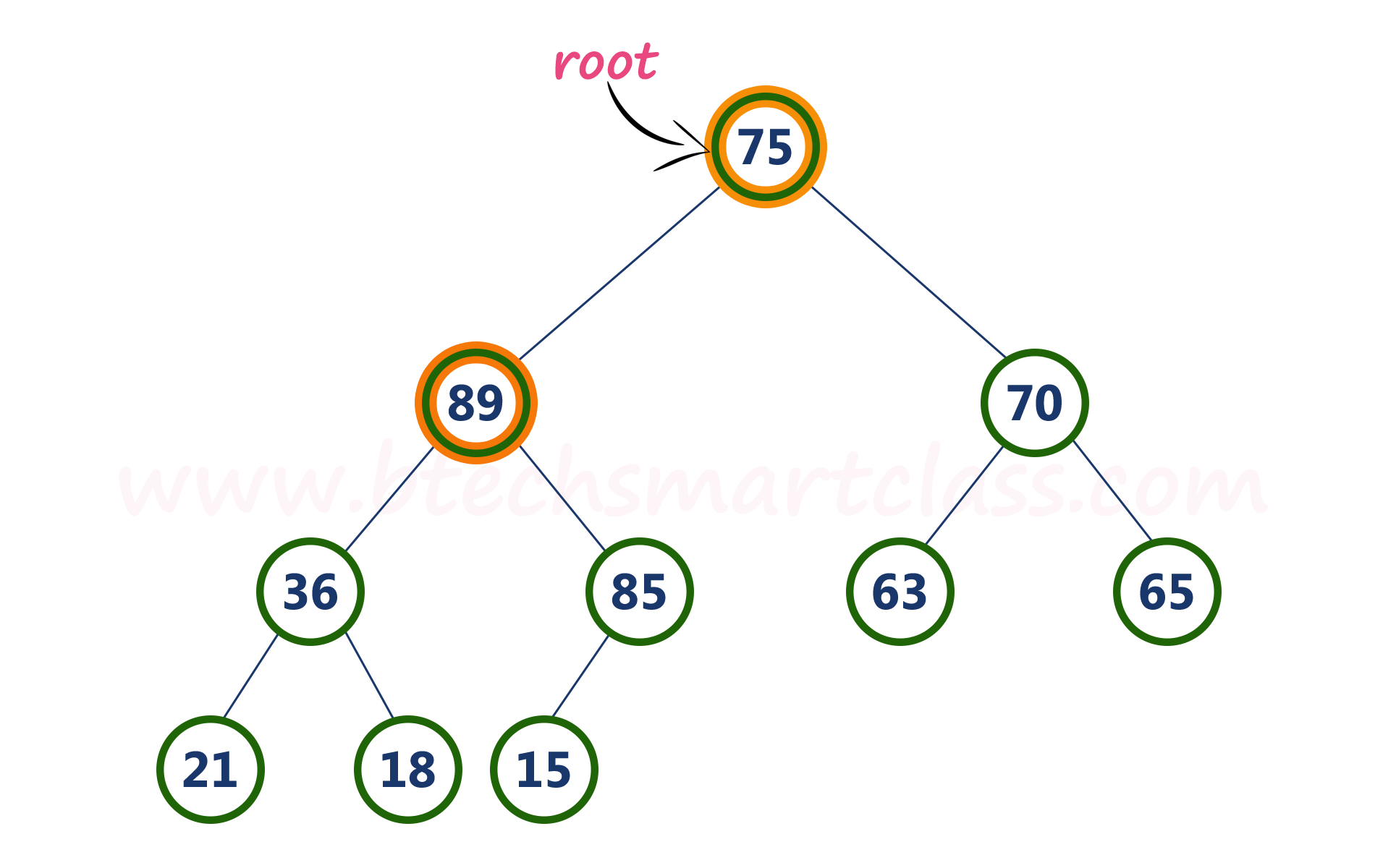
- Step 4 - Here, left child value (89) is larger than its right sibling (70), So, swap root (75) with left child (89).
- Step 5 - Now, again compare 75 with its left child (36).
- Step 6 - Here, node with value 75 is smaller than its right child (85). So, we swap both of them. After swapping max heap is as follows...
- Step 7 - Now, compare node with value 75 with its left child (15).
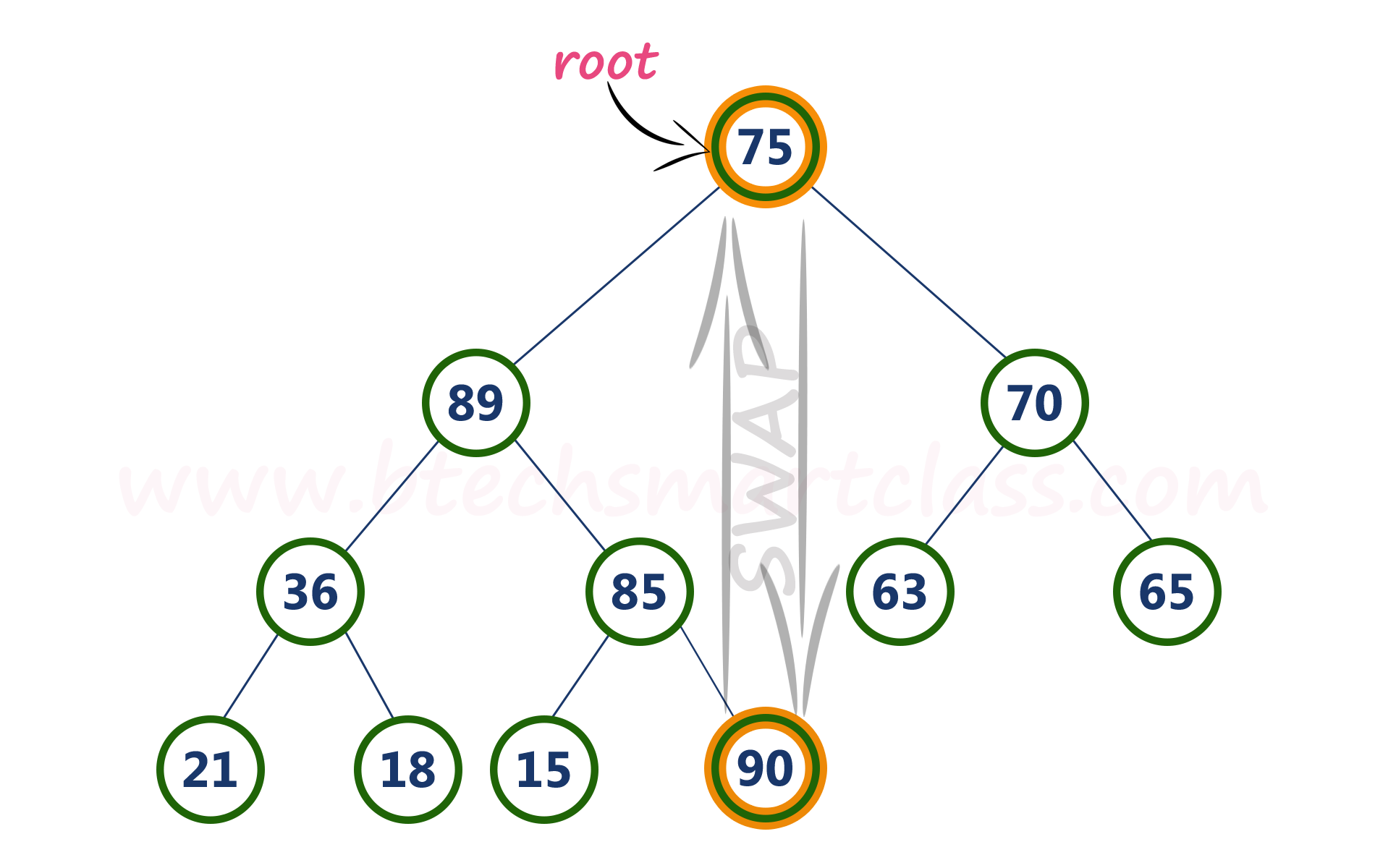
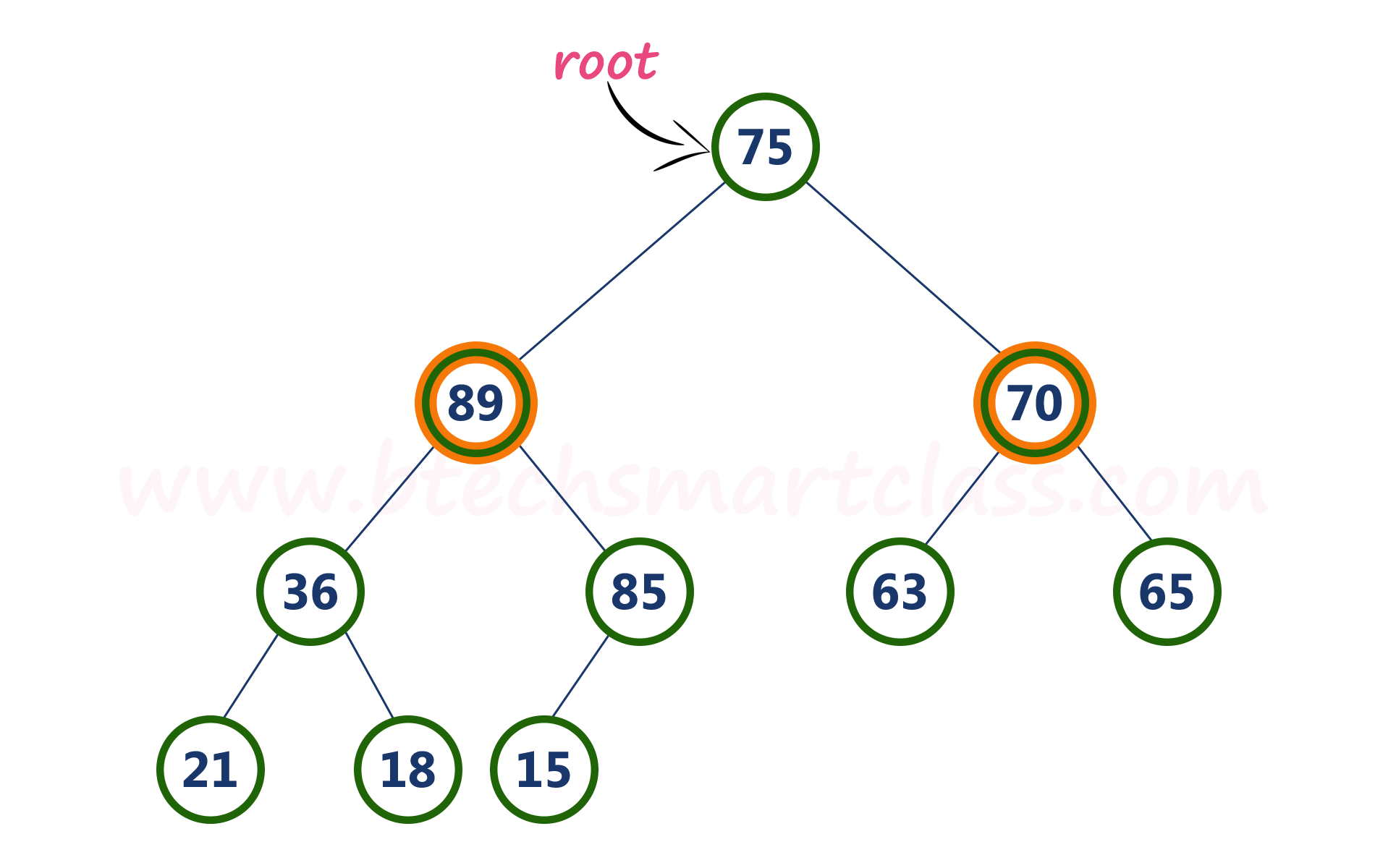
Here, root value (75) is smaller than its left child value (89). So, compare left child (89) with its right sibling (70).
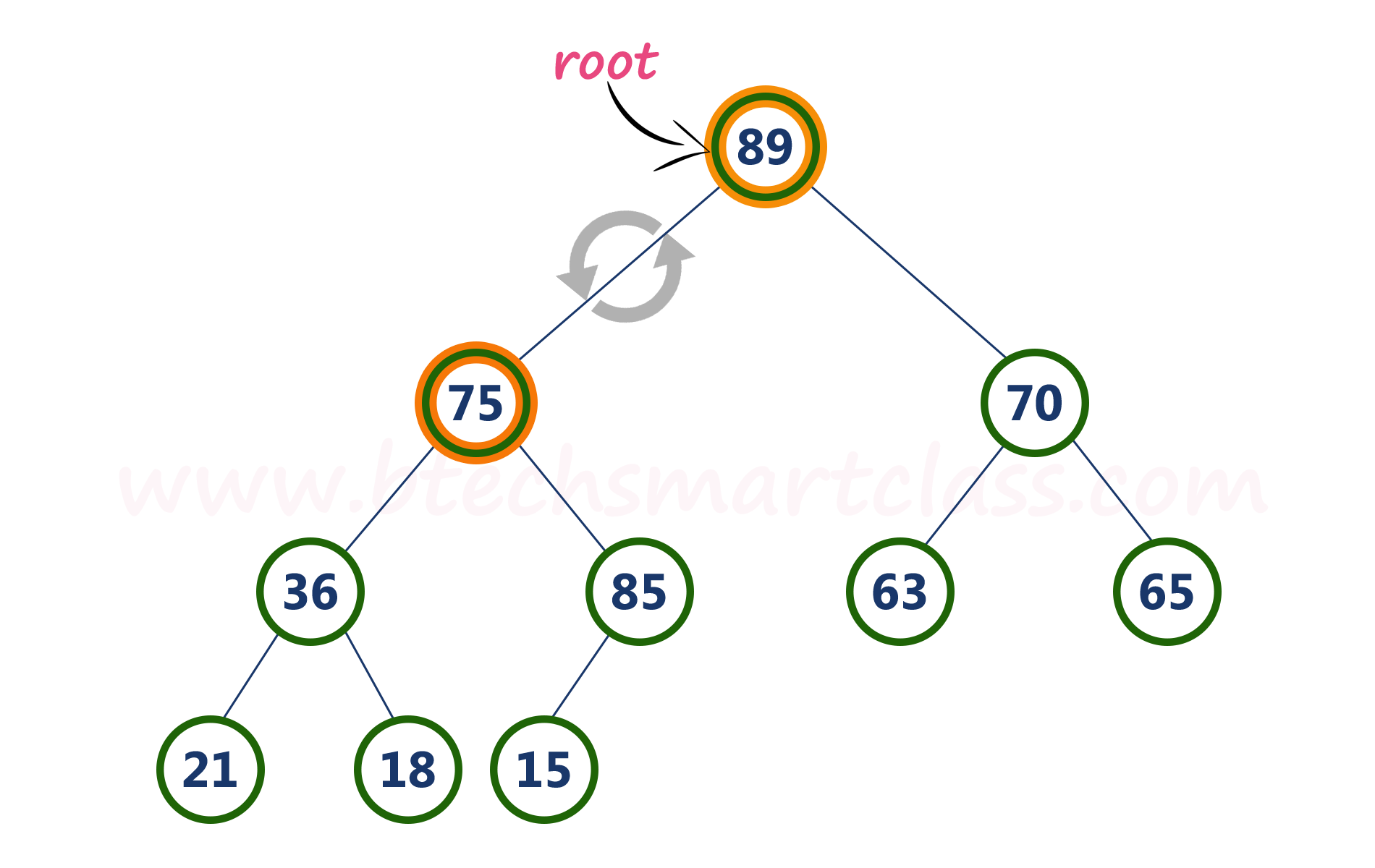
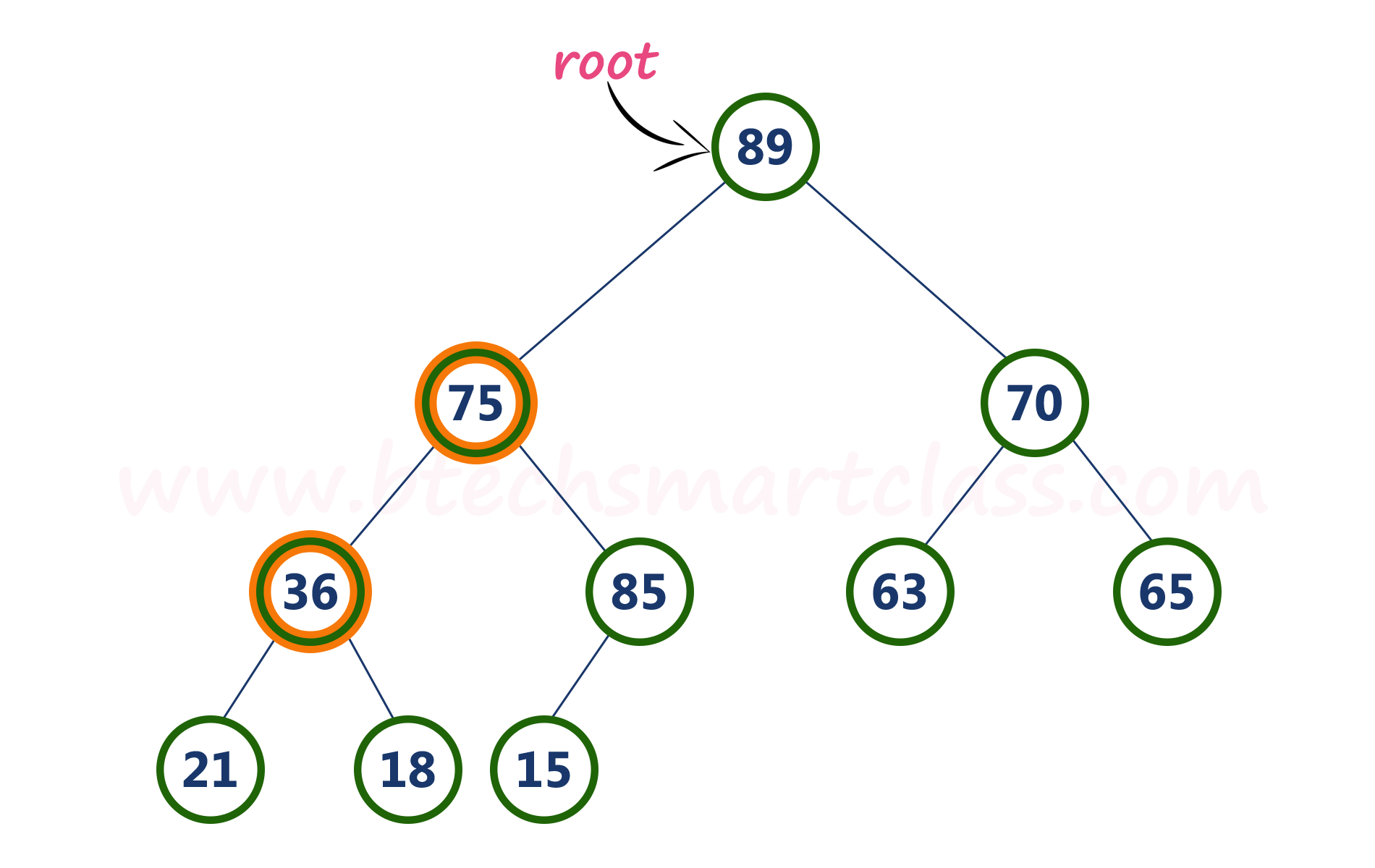
Here, node with value 75 is larger than its left child. So, we compare node 75 with its right child 85.
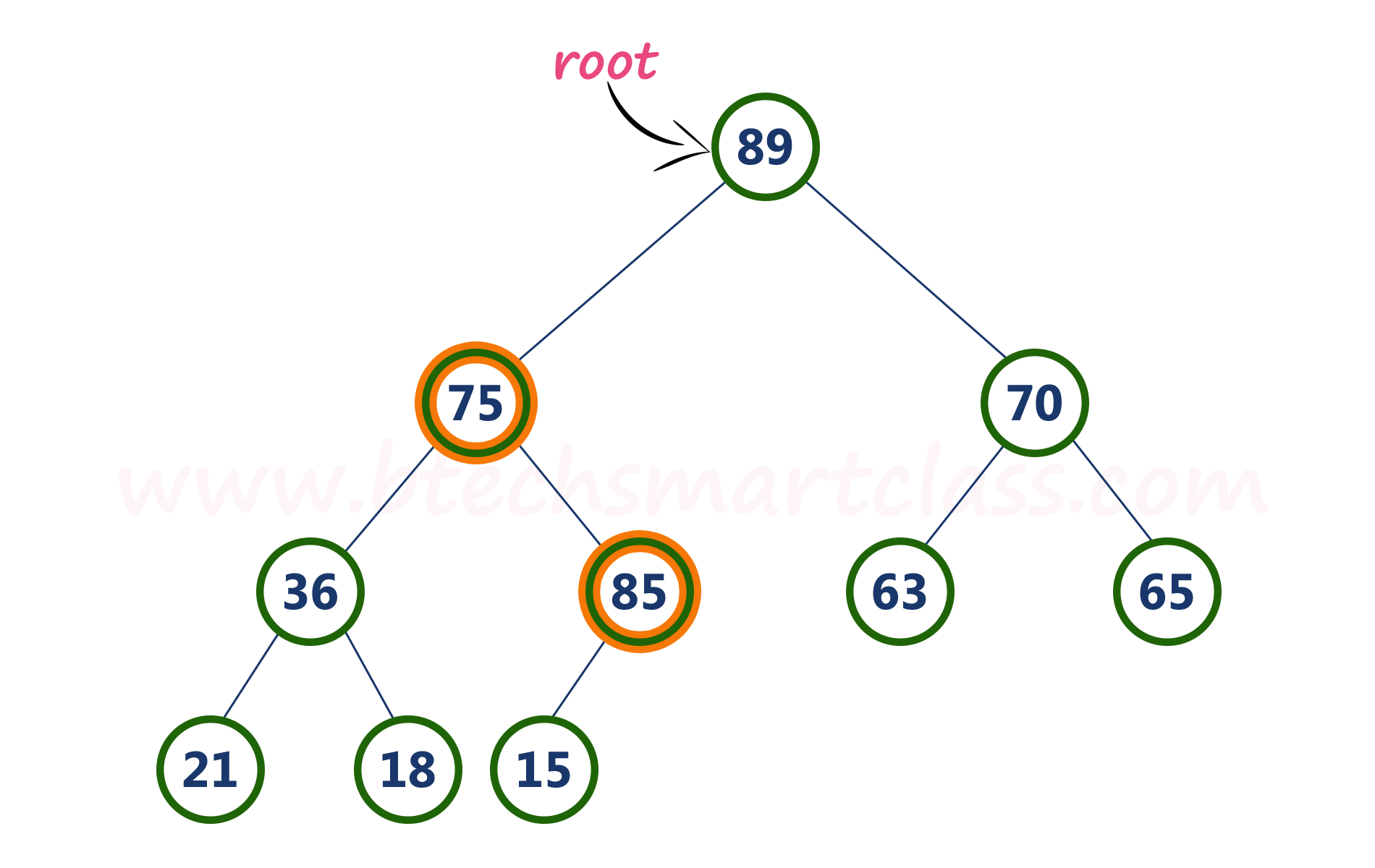
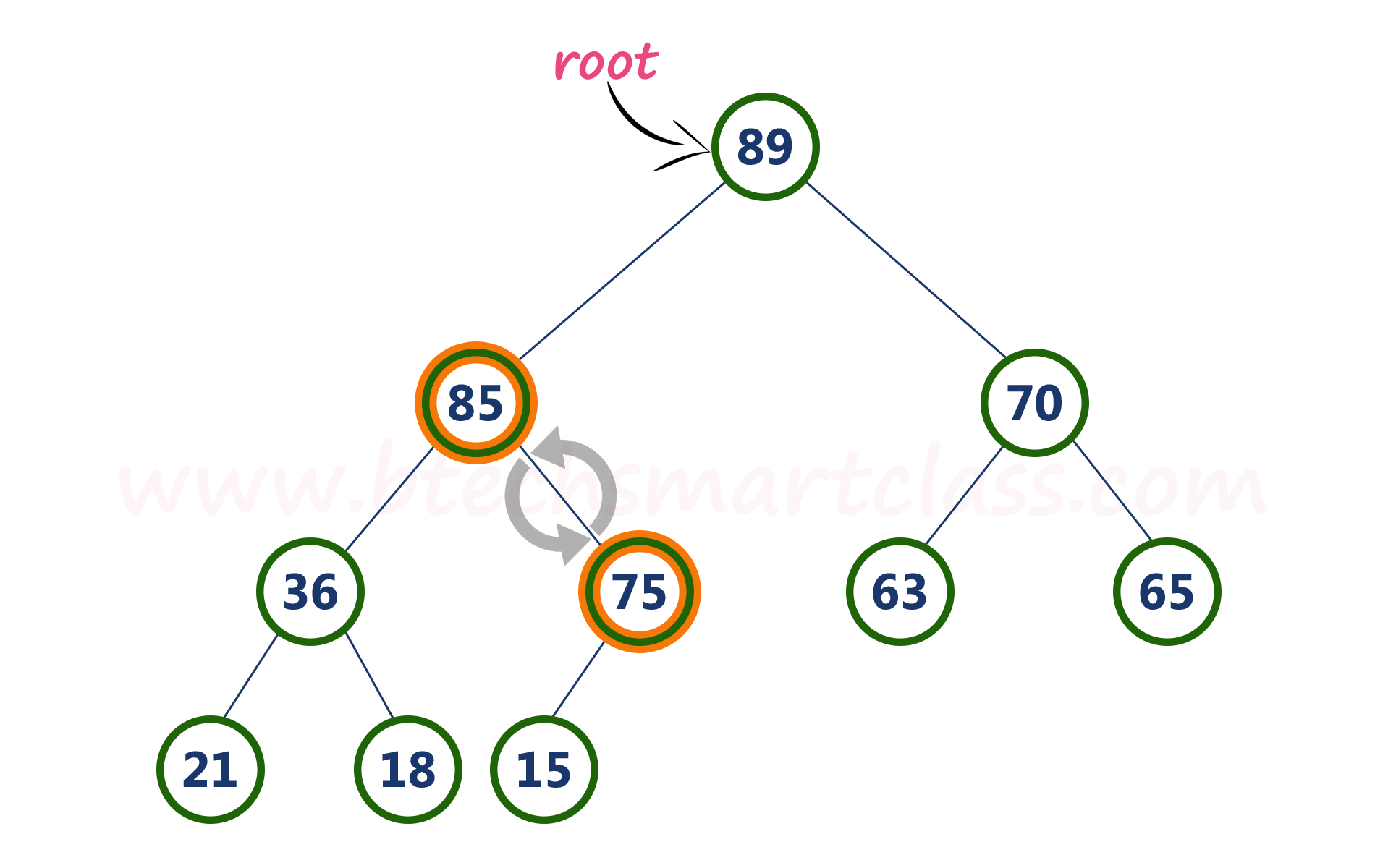
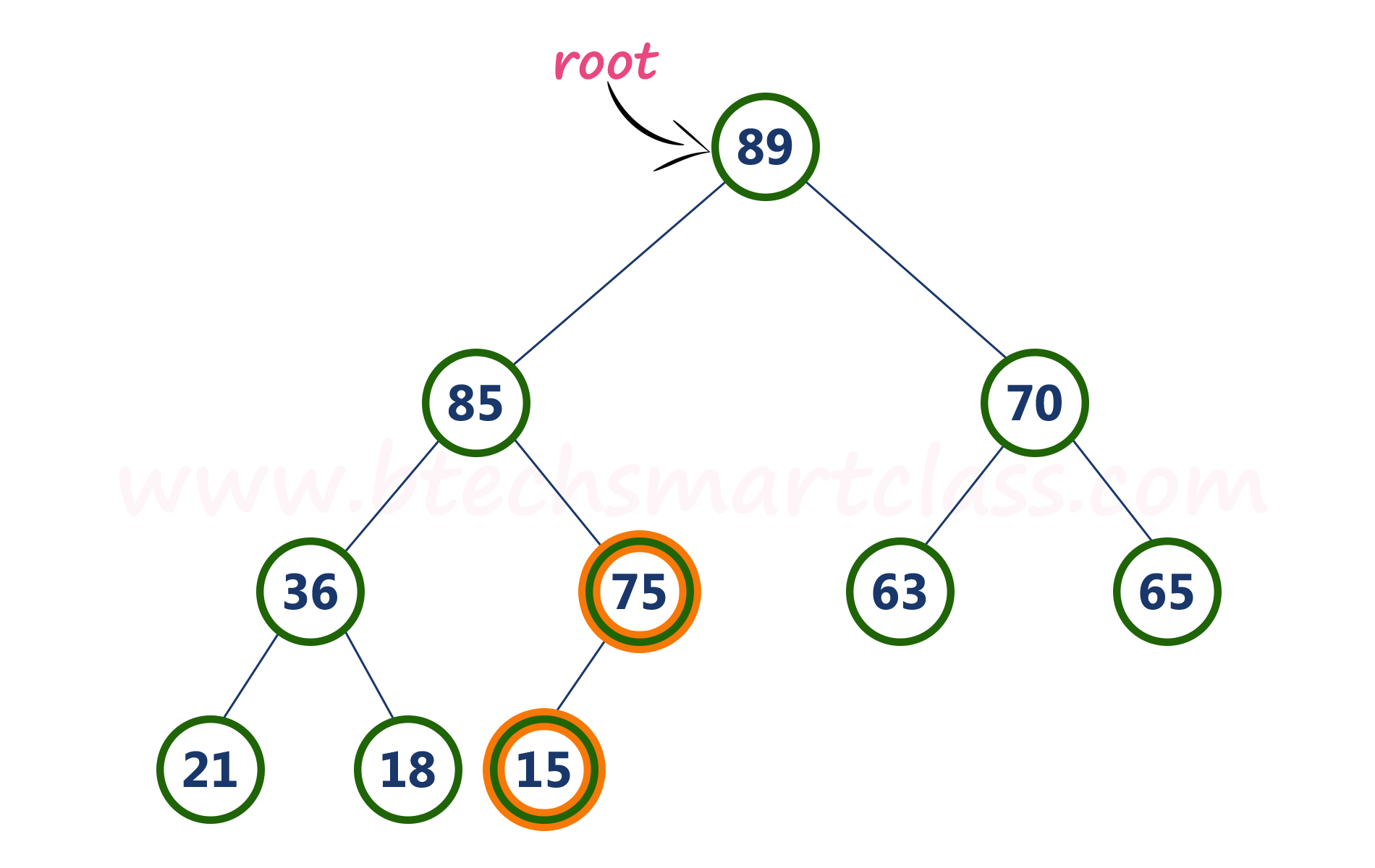
Here, node with value 75 is larger than its left child (15) and it does not have right child. So we stop the process.
Finally, max heap after deleting root node (90) is as follows...