Knuth-Morris-Pratt Algorithm
KMP Algorithm is one of the most popular patterns matching algorithms. KMP stands for Knuth Morris Pratt. KMP algorithm was invented by Donald Knuth and Vaughan Pratt together and independently by James H Morris in the year 1970. In the year 1977, all the three jointly published KMP Algorithm.
KMP algorithm was the first linear time complexity algorithm for string matching.
KMP algorithm is one of the string matching algorithms used to find a Pattern in a Text.
KMP algorithm is used to find a "Pattern" in a "Text". This algorithm campares character by character from left to right. But whenever a mismatch occurs, it uses a preprocessed table called "Prefix Table" to skip characters comparison while matching. Some times prefix table is also known as LPS Table. Here LPS stands for "Longest proper Prefix which is also Suffix".
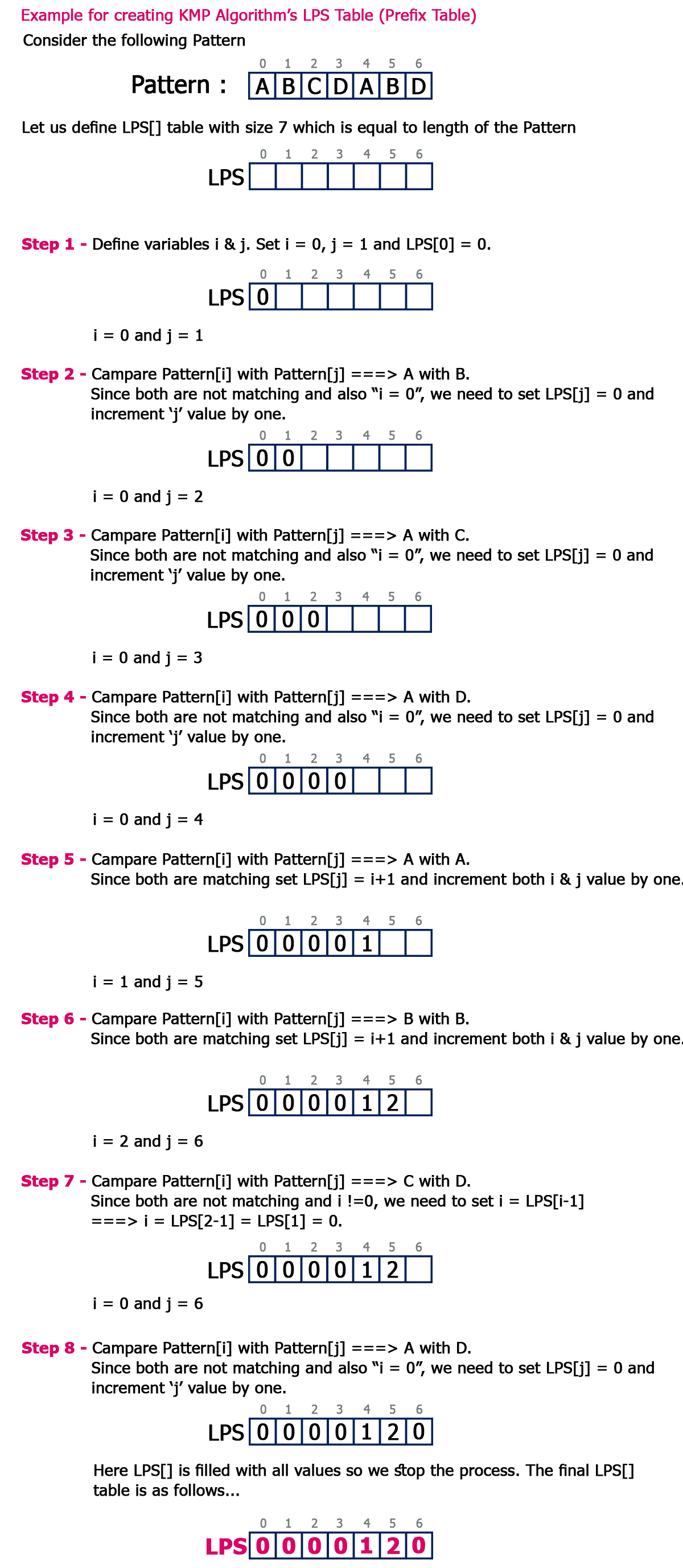
Steps for Creating LPS Table (Prefix Table)
- Step 1 - Define a one dimensional array with the size equal to the length of the Pattern. (LPS[size])
- Step 2 - Define variables i & j. Set i = 0, j = 1 and LPS[0] = 0.
- Step 3 - Compare the characters at Pattern[i] and Pattern[j].
- Step 4 - If both are matched then set LPS[j] = i+1 and increment both i & j values by one. Goto to Step 3.
- Step 5 - If both are not matched then check the value of variable 'i'. If it is '0' then set LPS[j] = 0 and increment 'j' value by one, if it is not '0' then set i = LPS[i-1]. Goto Step 3.
- Step 6- Repeat above steps until all the values of LPS[] are filled.
Let us use above steps to create prefix table for a pattern...
How to use LPS Table
We use the LPS table to decide how many characters are to be skipped for comparison when a mismatch has occurred.
When a mismatch occurs, check the LPS value of the previous character of the mismatched character in the pattern. If it is '0' then start comparing the first character of the pattern with the next character to the mismatched character in the text. If it is not '0' then start comparing the character which is at an index value equal to the LPS value of the previous character to the mismatched character in pattern with the mismatched character in the Text.
How the KMP Algorithm Works
Let us see a working example of KMP Algorithm to find a Pattern in a Text...

