Max Priority Queue
In the normal queue data structure, insertion is performed at the end of the queue and deletion is performed based on the FIFO principle. This queue implementation may not be suitable for all applications.
Consider a networking application where the server has to respond for requests from multiple clients using queue data structure. Assume four requests arrived at the queue in the order of R1, R2, R3 & R4 where R1 requires 20 units of time, R2 requires 2 units of time, R3 requires 10 units of time and R4 requires 5 units of time. A queue is as follows...
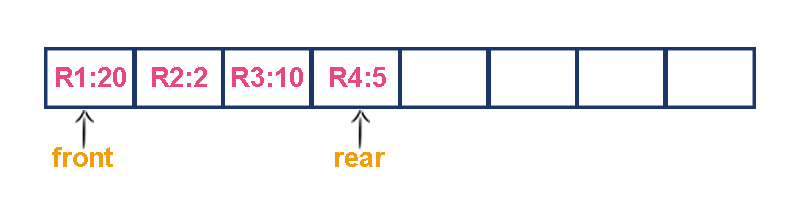
Now, check to wait time of each request that to be completed.
- R1 : 20 units of time
- R2 : 22 units of time (R2 must wait until R1 completes 20 units and R2 itself requires 2 units. Total 22 units)
- R3 : 32 units of time (R3 must wait until R2 completes 22 units and R3 itself requires 10 units. Total 32 units)
- R4 : 37 units of time (R4 must wait until R3 completes 35 units and R4 itself requires 5 units. Total 37 units)
That means, if we use a normal queue data structure to serve these requests the average waiting time for each request is 27 units of time.
Now, consider another way of serving these requests. If we serve according to their required amount of time, first we serve R2 which has minimum time (2 units) requirement. Then serve R4 which has second minimum time (5 units) requirement and then serve R3 which has third minimum time (10 units) requirement and finally R1 is served which has maximum time (20 units) requirement.
Now, check to wait time of each request that to be completed.
- R2 : 2 units of time
- R4 : 7 units of time (R4 must wait until R2 completes 2 units and R4 itself requires 5 units. Total 7 units)
- R3 : 17 units of time (R3 must wait until R4 completes 7 units and R3 itself requires 10 units. Total 17 units)
- R1 : 37 units of time (R1 must wait until R3 completes 17 units and R1 itself requires 20 units. Total 37 units)
From the above two situations, it is very clear that the second method server can complete all four requests with very less time compared to the first method. This is what exactly done by the priority queue.
Priority queue is a variant of a queue data structure in which insertion is performed in the order of arrival and deletion is performed based on the priority.
There are two types of priority queues they are as follows...
- Max Priority Queue
- Min Priority Queue
1. Max Priority Queue
In a max priority queue, elements are inserted in the order in which they arrive the queue and the maximum value is always removed first from the queue. For example, assume that we insert in the order 8, 3, 2 & 5 and they are removed in the order 8, 5, 3, 2.
The following are the operations performed in a Max priority queue...
- isEmpty() - Check whether queue is Empty.
- insert() - Inserts a new value into the queue.
- findMax() - Find maximum value in the queue.
- remove() - Delete maximum value from the queue.
Max Priority Queue Representations
There are 6 representations of max priority queue.
- Using an Unordered Array (Dynamic Array)
- Using an Unordered Array (Dynamic Array) with the index of the maximum value
- Using an Array (Dynamic Array) in Decreasing Order
- Using an Array (Dynamic Array) in Increasing Order
- Using Linked List in Increasing Order
- Using Unordered Linked List with reference to node with the maximum value
#1. Using an Unordered Array (Dynamic Array)
In this representation, elements are inserted according to their arrival order and the largest element is deleted first from the max priority queue.
For example, assume that elements are inserted in the order of 8, 2, 3 and 5. And they are removed in the order 8, 5, 3 and 2.
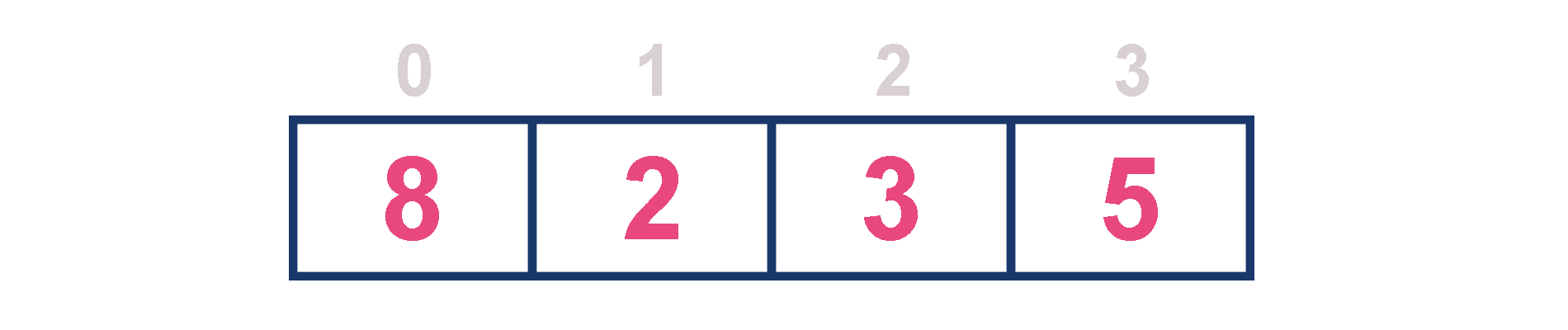
Now, let us analyze each operation according to this representation...
isEmpty() - If 'front == -1' queue is Empty. This operation requires O(1) time complexity which means constant time complexity.
insert() - New element is added at the end of the queue. This operation requires O(1) time complexity which means constant time complexity.
findMax() - To find the maximum element in the queue, we need to compare it with all the elements in the queue. This operation requires O(n) time complexity.
remove() - To remove an element from the max priority queue, first we need to find the largest element using findMax() which requires O(n) time complexity, then that element is deleted with constant time complexity O(1). The remove() operation requires O(n) + O(1) ≈ O(n) time complexity.
#2. Using an Unordered Array (Dynamic Array) with the index of the maximum value
In this representation, elements are inserted according to their arrival order and the largest element is deleted first from max priority queue.
For example, assume that elements are inserted in the order of 8, 2, 3 and 5. And they are removed in the order 8, 5, 3 and 2.
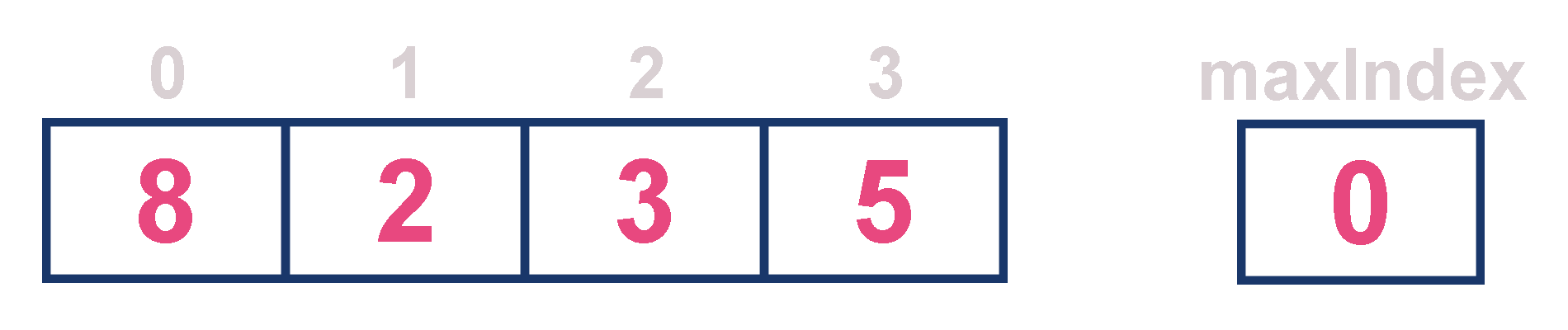
Now, let us analyze each operation according to this representation...
isEmpty() - If 'front == -1' queue is Empty. This operation requires O(1) time complexity which means constant time complexity.
insert() - New element is added at the end of the queue with O(1) time complexity and for each insertion we need to update maxIndex with O(1) time complexity. This operation requires O(1) time complexity which means constant time complexity.
findMax() - Finding the maximum element in the queue is very simple because index of the maximum element is stored in maxIndex. This operation requires O(1) time complexity.
remove() - To remove an element from the queue, first we need to find the largest element using findMax() which requires O(1) time complexity, then that element is deleted with constant time complexity O(1) and finally we need to update the next largest element index value in maxIndex which requires O(n) time complexity. The remove() operation requires O(1)+O(1)+O(n) ≈ O(n) time complexity.
#3. Using an Array (Dynamic Array) in Decreasing Order
In this representation, elements are inserted according to their value in decreasing order and largest element is deleted first from max priority queue.
For example, assume that elements are inserted in the order of 8, 5, 3 and 2. And they are removed in the order 8, 5, 3 and 2.
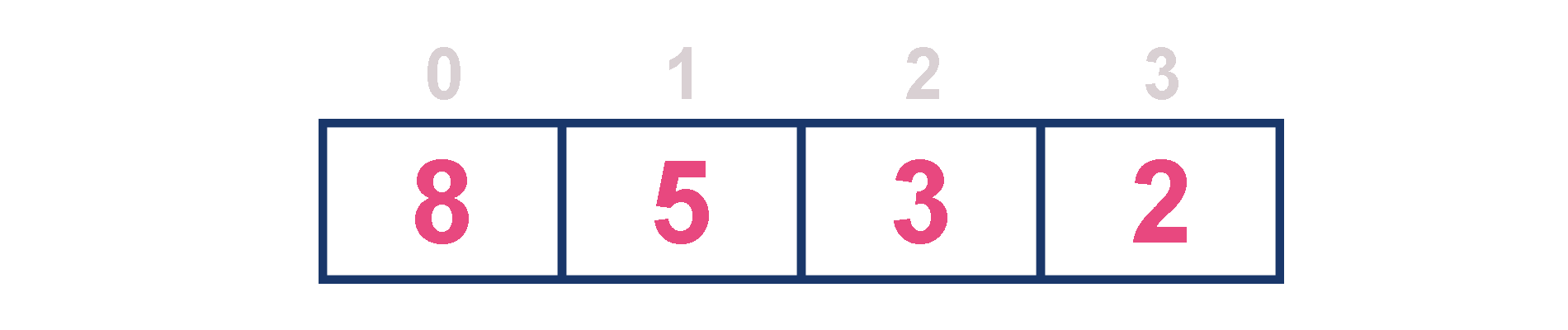
Now, let us analyze each operation according to this representation...
isEmpty() - If 'front == -1' queue is Empty. This operation requires O(1) time complexity which means constant time complexity.
insert() - New element is added at a particular position based on the decreasing order of elements which requires O(n) time complexity as it needs to shift existing elements inorder to insert new element in decreasing order. This insert() operation requires O(n) time complexity.
findMax() - Finding the maximum element in the queue is very simple because maximum element is at the beginning of the queue. This findMax() operation requires O(1) time complexity.
remove() - To remove an element from the max priority queue, first we need to find the largest element using findMax() operation which requires O(1) time complexity, then that element is deleted with constant time complexity O(1) and finally we need to rearrange the remaining elements in the list which requires O(n) time complexity. This remove() operation requires O(1) + O(1) + O(n) ≈ O(n) time complexity.
#4. Using an Array (Dynamic Array) in Increasing Order
In this representation, elements are inserted according to their value in increasing order and maximum element is deleted first from max priority queue.
For example, assume that elements are inserted in the order of 2, 3, 5 and 8. And they are removed in the order 8, 5, 3 and 2.
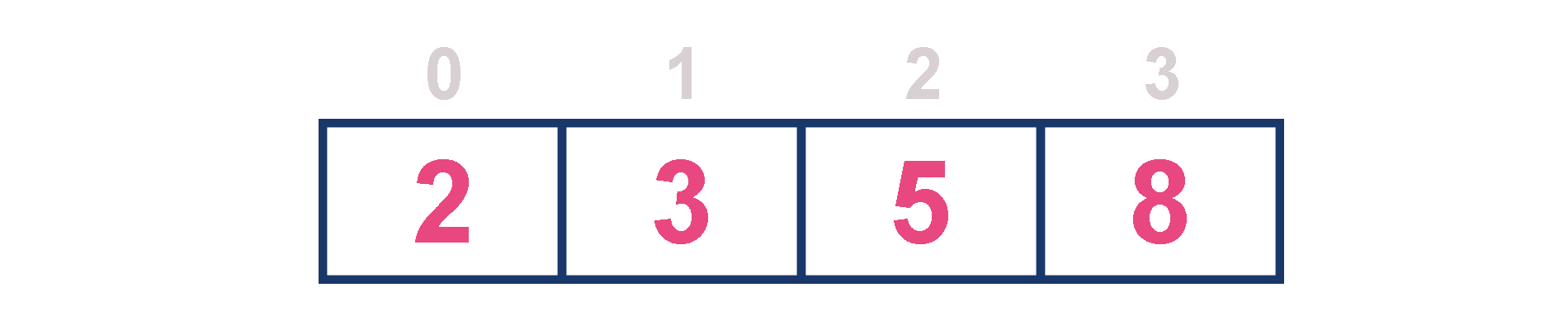
Now, let us analyze each operation according to this representation...
isEmpty() - If 'front == -1' queue is Empty. This operation requires O(1) time complexity which means constant time complexity.
insert() - New element is added at a particular position in the increasing order of elements into the queue which requires O(n) time complexity as it needs to shift existing elements to maintain increasing order of elements. This insert() operation requires O(n) time complexity.
findMax() - Finding the maximum element in the queue is very simple becuase maximum element is at the end of the queue. This findMax() operation requires O(1) time complexity.
remove() - To remove an element from the queue first we need to find the largest element using findMax() which requires O(1) time complexity, then that element is deleted with constant time complexity O(1). Finally, we need to rearrange the remaining elements to maintain increasing order of elements which requires O(n) time complexity. This remove() operation requires O(1) + O(1) + O(n) ≈ O(n) time complexity.
#5. Using Linked List in Increasing Order
In this representation, we use a single linked list to represent max priority queue. In this representation, elements are inserted according to their value in increasing order and a node with the maximum value is deleted first from the max priority queue.
For example, assume that elements are inserted in the order of 2, 3, 5 and 8. And they are removed in the order of 8, 5, 3 and 2.
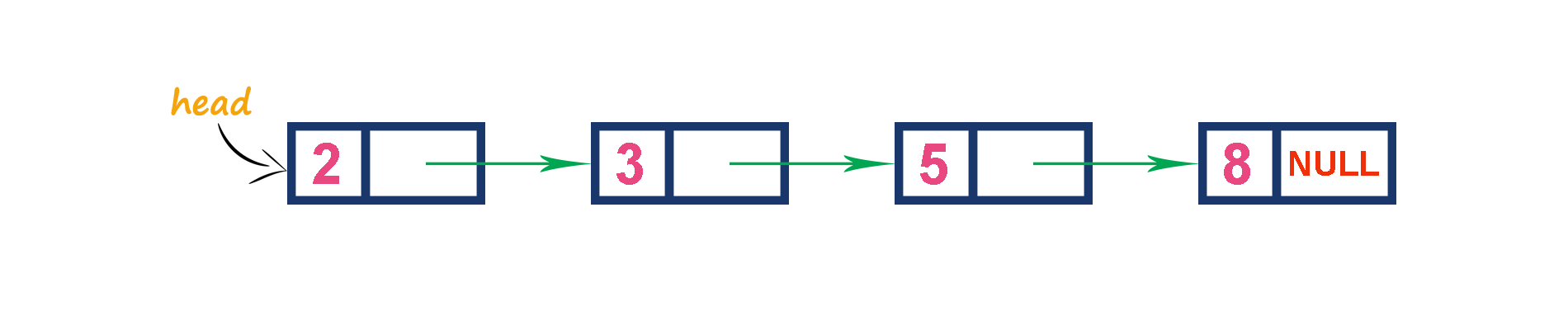
Now, let us analyze each operation according to this representation...
isEmpty() - If 'head == NULL' queue is Empty. This operation requires O(1) time complexity which means constant time complexity.
insert() - New element is added at a particular position in the increasing order of elements which requires O(n) time complexity. This insert() operation requires O(n) time complexity.
findMax() - Finding the maximum element in the queue is very simple because maximum element is at the end of the queue. This findMax() operation requires O(1) time complexity.
remove() - Removing an element from the queue is simple because the largest element is last node in the queue. This remove() operation requires O(1) time complexity.
#6. Using Unordered Linked List with reference to node with the maximum value
In this representation, we use a single linked list to represent max priority queue. We always maintain a reference (maxValue) to the node with the maximum value in the queue. In this representation, elements are inserted according to their arrival and the node with the maximum value is deleted first from the max priority queue.
For example, assume that elements are inserted in the order of 2, 8, 3 and 5. And they are removed in the order of 8, 5, 3 and 2.
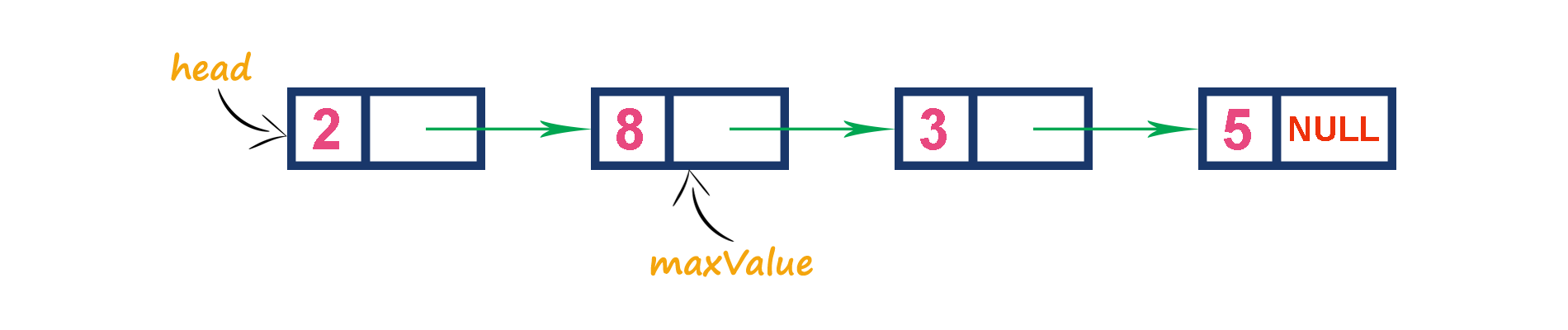
Now, let us analyze each operation according to this representation...
isEmpty() - If 'head == NULL' queue is Empty. This operation requires O(1) time complexity which means constant time complexity.
insert() - New element is added at end of the queue which requires O(1) time complexity. And we need to update maxValue reference with address of largest element in the queue which requires O(1) time complexity. This insert() operation requires O(1) time complexity.
findMax() - Finding the maximum element in the queue is very simple because the address of largest element is stored at maxValue. This findMax() operation requires O(1) time complexity.
remove() - Removing an element from the queue is deleting the node which is referenced by maxValue which requires O(1) time complexity. And then we need to update maxValue reference to new node with maximum value in the queue which requires O(n) time complexity. This remove() operation requires O(n) time complexity.
2. Min Priority Queue Representations
Min Priority Queue is similar to max priority queue except for the removal of maximum element first. We remove minimum element first in the min-priority queue.
The following operations are performed in Min Priority Queue...
- isEmpty() - Check whether queue is Empty.
- insert() - Inserts a new value into the queue.
- findMin() - Find minimum value in the queue.
- remove() - Delete minimum value from the queue.
